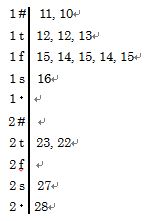白瀧と申します。
先日はセミナ「ばらつきを診れば品質が見えてくる」で大変お世話になりました。
ここで質問するのも場違いかと思いましたが、折角なので質問させて下さい。
セミナ当日に頂いたテキストに沿ってexcel2010で箱ひげ図を描こうとしていますが
以下のようなエラーが出て、先に進めません。
環境的なものだとは思いますが、ご教示頂ければ幸いです。
（ネットで調べてみましたが、同じような現象が出ている方はいるものの
具体的な解決策までは探せませんでした。）
エラーが発生するタイミングは「その他のグラフ」から「株価チャート（始値－高値－安値－終値）」を
選択したときです。
「この株価チャートを作成するには、始値、高値、安値、終値の順でシートのデータを配置してください。
ラベルには、日付または銘柄を使用してください。」
データは以下の通りです
2010 2011 2012
第一 0.088 0.065 0.03
最大 0.81 0.66 0.41
最小 0.04 0.01 0.004
第三 0.605 0.4 0.21
以上、よろしくお願いします。
プロセス改善フォーラム事務局の堀田です。
10月11日（金）14:00から、3周年記念イベントとして、『ＩＴ異色経験者５人による「改善のコツと進め方のアドバイス」～来てみて、聞いてみて、相談してヒントを掴んでみませんか』というセミナー（ちょっと長いですが）を開催することになりました。 CMM v1.1が発行されてからちょうど20年になります。CMMは瞬く間に世界中に広がり、ソフトウェアに従事する者は知らない人はいないくらいになりました。プロセスとその能力という視点は「目からうろこ」のインパクトを人々に与えました。この流れは国際標準化にも及び、今や、ソフトウェアの世界ではISO9001と並んでCMMI、ISO15504が多く使われています。その意味で、CMMは、まさに歴史的なエポックメイキングだったのではないかと思います。一方、CMMが本当にうまく使われ、効果を上げてきたかというと、疑問に思う人も多くおられるのではないかと思います。しかしながら、 ISO9001にしろCMMにしろ、モデル自体がおかしいことを言っているかというとそうではないと思います。問題はその使い方にあるのではないでしょうか。このセミナーでは、これまで長い間、改善に何かしらの関わりをもった各方面の関係者がそれぞれに自らの経験を通じて培った知見を、議論のきっかけとしてお話しし、その後、自由形式で意見交換をするという、パネルディスカッション風のアレンジで、ただし、発表者だけが意見を交わすのではなく、会場に集まった全員が参加することを想定しています。そのため、懇談会はできるだけリラックスした形で行えるように工夫します。議論を通じて、何らかのヒントを得ていただくことができれば成功です。参加費には、セミナー資料と懇談会の費用が含まれます。
ご興味のある方は、こちらからお申込ください。
皆様とお会いしお話できることを楽しみにしております。
「「わくわく」感を生み出す人間重視の品質改善実践法 ― 品質マインド醸成法と改善活動への動機付けのコツ －」の講師の関です。
「ほんの少し」当日の内容をご紹介しましょう・・・・・・。
不具合や人的ミス等による品質問題は依然と後を絶たず、増々深刻化してきており、より効果的、効率的な改善方法が求められています。多くの企業は、ひとたび失敗すると振り返りを迫り、監査や検査を強化して「言われたことしかやらない」、「考えない集団」を生み出し「負の連鎖」を繰り返してしまいます。このような状況を断ち切る鍵は「人間重視の品質改善」にあると考え実践して効果を上げてきました。
■「改善を実施しない人々を動かすには？」：以下の状況の時にどうすれば良いでしょうか？
●ケース１：リーダが強引に品質改善を推進してCMMI®のレベルを達成して評価された。しかし、看板獲得の活動に終始し組織メンバーは疲弊していて「２度と改善をやりたくない」と思っている。
●ケース２：あるトラブルをきっかけに、改善活動を開始することになったが、「そんな事を実施する時間がない」等と反対の人が多い。
このような場合、マネージメント手法として「報酬や命令で人々を動かそう」としてきましたが、そのような成長期を基盤にした古い手法では、組織的活動は進展しません。そこには「企業の意志」はあっても肝心の「社員の意志」が伴わない改善活動が展開されてしまっているのです。
■「人間力の醸成と発揮の効果」：命令しなくても人が動き出す。
「人間力」を重視した仕組みを考案できると、命令しなくても人々を主目的の活動に向かわせることが可能になります。また、単に動き出すだけでなく、「人間重視の改善活動」が「わくわく」感を生み出し、人々を自立から真の自律化に進化させることが可能になります。
本ワークショップでは、「人間力醸成」を基盤にした「人を動かす仕組み考案のコツ」、「品質マインド醸成法」、「改善活動への動機付け法」、「具体的な人を動かす仕組のデザイン事例」等について、多くの演習を体験していただき、職場での実践に役立つ内容にしたいと考えております。
私は「組織的活動は組織に価値をもたらすと共に個々人の価値観『わくわく』感と『生きがい』を生み出すものでなければならない」と考えております。
☆「本当に実現するの???」との疑問や関心を持たれた方や今まで様々な方法論を試してみたが、なかなか効果が早く表れないと悩んでいらっしゃる方々・・・・是非、ご参加いただき、体験し、実践に役立てていただければ幸いです・・・・。コンサルやセミナー、ワークショップ受講等を通じて多くの方々に実践へのヒントを会得していただいております。
® Capability Maturity Model、CMM、CMMI は、カーネギーメロン大学によって米国特許商標庁に登録されています。
１月２４日のワークショップ「小規模開発向け軽量プロセスのすすめ― 顧客信頼向上に役立つVSE標準の活用 ―」の講師の伏見です。
ソフトウェア開発の現場は、しばしば、小規模な開発組織、開発企業が担当しています。また、短期間開発の比重も高まってきました。そうした現場の作業環境は、なかなか高度化されず、いわゆる「現場の疲弊」が蔓延しているといわれます。疲弊の結果、現場の人々が明日の納期のことしか考えられなくなると、ますます泥沼的な作業に陥っていきます。開発技量が育成されないケース、開発環境が十分でないケース、開発環境はあっても有効に活用されないケース、いろいろな閉塞状況が懸念されます。かといって、あまり大げさに開発プロセスの改革にとりくむのも大変です。
幸い、最近、小規模組織向けの開発（プロセス）国際標準が開発されました。１月のワークショプでは、この標準の活用により組織の信頼性を高める方策を共に考えながら、国際討議、ＪＩＳ化討議の結果等もふまえた活用法の基本的な着眼点をお伝えしたいと思います。明日の開発力向上、信頼性向上のためにぜひご参加ください。
来年３月８日のワークショップ「あなたのデータ分析法は間違っていませんか？~ ロバスト統計手法のすすめ ~」の講師を務める宮﨑です。
ソフトウェアは人間が知恵を絞って一つずつ作ります。機械を使って工場で大量に生産できるわけではありません。一つずつ、作る人も違うし、作る物も違います。ソフトウェアも一般工業製品のような機械的管理ができるのではないかという願望のもとに、管理図等の手法を導入しようという試みは、長い間なされてきましたが成功したと言える組織はどの程度あるのでしょうか。ソフトウェア開発にはあまりにも変動要因が多いのです。そして、技術の進歩の速さが、ソフトウェア開発をますます多様にします。ソフトウェアという多様性のある製品を、多様なプロセスで開発する過程から出てくるデータは、多様性のかたまりです。このようなデータを従来の統計的手法で扱っていたのでは、間違いをおこす確率が高くなります。３月８日のワークショップでは、ソフトウェア開発のデータをより適切に分析できる統計手法について、事例と演習により理解を深めていただきたいと思っています。皆様、奮ってご参加ください。
事務所前のおかめ桜
秋も深まり、事務所前のおかめ桜も紅葉しています。
昨日の雨の後、今日は気持ちのよい晴天です。
2周年記念イベント“プロセス改善の集い”には多くのご参加をいただき、ありがとうございました。講演や意見交換では、ISO26262を取り巻く欧州、日本の動向に加え、ISO26262の意義、企業文化醸成の必要性、対応策等について語られ、有意義な半日でした。今回、機会を逸した方も含めて、次回をご期待ください。
さて、フォーラムでは1月から3月にかけて以下のワークショップを予定しています。他ではなかなか得られない内容豊富なコースです。皆様のご参加をお待ちしております。
●小規模開発向け軽量プロセスのすすめ－顧客信頼向上に役立つVSE標準の活用
2013年01月２4日（木） 講師 伏見 諭（ふしみ さとし）氏
●～ITも心の時代へ～ 「わくわく」感を生み出す人間重視の品質改善実践法
―品質マインド醸成法と改善活動への動機付けのコツ－
2013年02月08日（金） 講師 関 弘充（せき ひろみつ）氏
●あなたのデータ分析法は間違っていませんか？ ～ロバスト統計手法のすすめ～
2013年03月08日（金） 講師 宮崎 幸生（みやざき ゆきお）氏
プロセス改善フォーラム事務局の堀田です。学校も夏休みに入り、暑い日が続いていますが、皆様お元気でお過ごしでしょうか。
時が過ぎるのは早いもので、プロセス改善フォーラムも発足して既に2年近くが経過しました。これまでご参加、ご協力いただいた皆様には深く感謝申し上げます。
そこで、3ヶ月くらい先の話になりますが、2周年記念として、以下の集いを企画いたしました。万障お繰り合わせの上、是非ご参加いただけば幸です。この会はオープンな会ですので、どなたでも、勿論初めてご参加の方も歓迎です。席に限りがありますのでお早めにお申込ください。
(1)「プロセス改善フォーラム」2周年記念イベント
“プロセス改善の集い” 「ISO26262機能安全」最新情報と関連モデルの活用
– 最新情報を入手、そして真の効果に繋げるために
トップ講師による「ISO 26262機能安全」に関する最新情報や関連モデルの活用に向けたセミナーと意見交換の会を開催します。
10月 23日（火） 14:30～18:00
講師： 小谷田 一詞 （（財）日本自動車研究所）
白 石 肇 （白石ソフトウェアプロセス改善ワークショップ）
また、ご好評にお応えしての第二弾、記念イベントと合わせ皆様のご参加をお待ちしております。
(2) 直ぐにソフトウェア品質を良くするコツ ― 短期成果追求型の品質改善実践法 ―
講師： 関 弘充 （ヒューマン＆クオリティ・ラボ） 10月24日（水） 10:30～17：30
(3)統計学を知らなくてもできる定量的データ分析 ～ナイチンゲールに学ぶデータ分析術～
講師： 宮崎幸生 （富士通クオリティ・ラボ） 11月9日（金） 10:30～17：30
第２章に登場するのは５数要約 (5-number summary) と箱ひげ図 (box-and-whisker
plot) です。まず、５数要約について、以下のソフトウェアシステムの構成要素毎の詳細
設計レビュー工数（人時）を使って説明します。
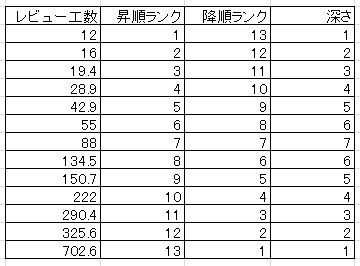
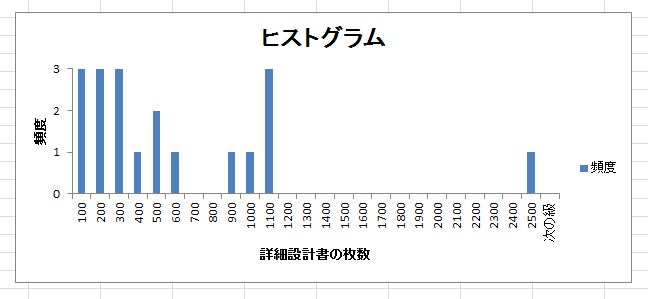
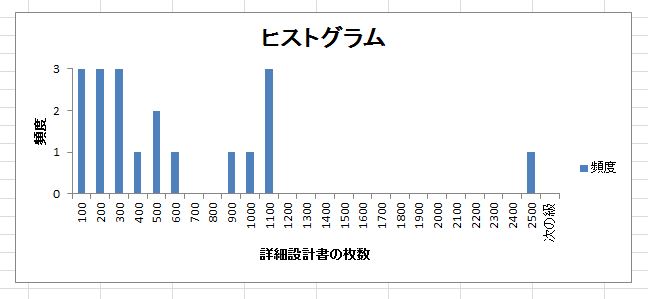
一番左の列がレビュー工数のデータです。その右が小さいもの順につけた順位で、その右
が逆に大きいもの順につけた順位です。一番右の列が昇順ランクと降順ランクの小さい方
をとった「深さ」になります。このデータを、５数要約の基本形で表現すると、次のよう
になります。
#13はデータの件数です。下向きの箱の中に入っている５つの数字が５数ということにな
ります。 小さい方から数えても大きい方から数えても同じ７という順位になるのが中央
値 (median) です。順位の最小値１と最大値１３を足して２で割っても同じ答えは出てき
ます。５数要約では、Ｍ７（Medianは深さ７)の右、下向きの箱の上部に８８と書きま
す。
中央値の考え方を延長し、中央値と最小値の真ん中のデータを求めます。深さから計算す
ると（１＋７）／２＝４となり、２８．９ということが分かります。中央値と最大値の真
ん中のデータも深さ４となり、２２２ということが分かります。この二つのデータをヒン
ジ (hinge) と言います。５数要約ではＨ４ (Hingeは深さ４)の右に小さい順に書きます。
最後に、深さ１の最小値と最大値を書いて、５数要約は完成します。
５数要約では、外れ値に関するルールと表記法も定めています。
・「Ｈ幅 (H-spread)」＝二つのヒンジの差
・「ステップ (step)」＝ 1.5×Ｈ幅
・「内壁 (inner fences)」：ヒンジの１ステップ外側
つまり、内壁は二つあり一つは、最大値側のヒンジ＋ステップ
もう一つは、最小値側のヒンジ－ステップ
・「外壁 (outer fences)」：ヒンジの２ステップ外側
つまり、外壁も二つあり一つは、最大値側のヒンジ＋ 2×ステップ
もう一つは、最小値側のヒンジ－ 2×ステップ
としたときに、
◇ 内壁の内側にあるデータの最大値と最小値を内壁隣接値 (adjacent)
◇ 内壁と外壁の間にあるデータを外れ値 (outside)
◇外壁の外側にあるデータを度外れ値 (far out)
と定めています。このルールに従って、レビュー工数のデータでそれぞれを求めてみると
以下のようになります。
・Ｈ幅＝222－28.9＝193.1
・ステップ＝1.5×193.1＝289.65
・内壁の最大値側：222＋289.65＝511.65
・内壁の最小値側：28.9－289.65＝-260.75
・外壁の最大値側：222＋2×289.65＝801.3
・外壁の最小値側：28.9－2×289.65＝-550.4
◇内壁隣接値：12, 325.6
◇外れ値：702.6
◇度外れ値：なし
５数要約の基本形に、内壁、外壁、内壁隣接値、外れ値等を書き加えた表記法が以下です。
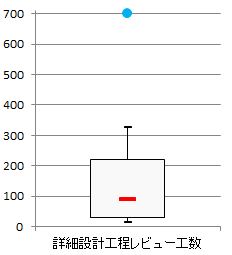
これらのデータが揃うと箱ひげ図が描けます。箱ひげ図は二つのヒンジを上辺、下辺とす
る箱の中に、中央値を描き、上辺、下辺から内壁隣接値までをひげのような線で結んだ図
です。以下に、上記データを使って箱ひげ図の例を示します。箱から伸びた上下のひげの
末端にある黒い ▬ が内壁隣接値で、赤い ▬ が中央値、青い ● が外れ値です。
今回は、５数要約と箱ひげ図の紹介をしました。なお、EXCELのQUARTILE関数により
計算される四分位数は、データ件数にもよりますが、テューキーのヒンジの計算結果と多
少異なります。EXCELやRが普及したこともあって、最近の書籍では、箱ひげ図の上辺
や下辺の定義にはEXCEL等による四分位数を使うことが多いようです。
前回はヒストグラムの説明をしました。今回は、いよいよ探索的データ解析の中身に入っていきます。第１章に登場するのが幹葉図 (stem-and-leaf) です。幹葉図は、カンヨウズと読んだりミキハズと読んだりするようです。前回のヒストグラムの説明で使った、以下のソフトウェアシステムの構成要素毎の詳細設計書枚数で、幹葉図を描いてみます。
285, 38, 321, 1060, 501, 1080, 136, 265, 106, 986, 45, 471, 422, 185, 1072, 269,
889, 2453, 82
幹葉図を描くのにExcelは不要で、単に次のようにデータを並べればよいのです。
**には00～99の数字が入ります。例えば1**は、100枚～199枚というヒストグラムで言えば一つの区間を意味します。同様に、***には000～999の数字が入ります。幹葉図の作り方は、データの最小値と最大値を考慮し、まず、縦線の左側に0**から2***までの区間を作っておきます。このようにしておけば、後は数字が並んでいる順 (285, 38, 321, ・・・, 82) に各区間にデータの下２桁（1000以上になったら下３桁）をコンマで区切って描いていけばよいのです。こうすることで、データを大きさの順に並べ変えるといったことはしなくても、間違えることは少なくなります。
以下は、前回のヒストグラムです。
お分かりのように、ヒストグラムを縦にするとほぼ幹葉図になります。ヒストグラムの各棒の長さが、幹葉図の縦線の右側の数字の数になることが分かります。ほぼ幹葉図と書いたのは、この幹葉図だとヒストグラムに比べて外れ値は一見分かりにくくなるからです。幹葉図の場合には、*の数に気を付けなければなりません。9**までは区間の幅は100なのですが、1***からは区間の幅が1000になるのです。したがって、ヒストグラムと同じイメージを保ちたければ、区間の幅を10**, 11**, 12** ・・・と最後まで100で統一すればよいのです。かなりのスペースはとることになりますが、ヒストグラムと同様の図にすることができます。
ヒストグラムだと元のデータの正確な値は分かりませんが、幹葉図なら分かります。並べ方を工夫しただけで、元のデータをそのまま描いたのが幹葉図なのです。この単純な発想の素晴らしさには脱帽です。
ヒストグラムのときに悩む区間の幅についても、幹葉図であれば悩むことはありません。10とか100といった幅で描くことになるのです。しかし、10や100だと粗過ぎて分布がよく分からない、という場合には、英語民族の発想ではありますが、次のようなアイディアも書かれています。
# ：0と1 注）参照
t ：2 (two) と3 (three)
f ：4 (four) と5 (five)
s ：6 (six) と7 (seven)
・：8と9
例えば、以下のようなデータがあったとします。
27, 28, 15, 23, 14, 12, 12, 15, 16, 11, 22, 14, 15, 13, 10
これを、以下の幹葉図にします。
これでは分布がよく分からないというときに、次のようにします。
これで、分布が少し見えてくるというわけです。
探索的データ解析には、この他にも様々な表現方法を使った幹葉図が、これでもかというほど出てきます。ちょっとした工夫で、どんなデータにでも使えるから考えてごらん、と言われているような気になります。
注）原著は0と1の記号は、# ではなく* を使っています。今回のブログでは * は、0～9の意味で統一した方が分かりやすいと思いましたので # を使いました。
私が今、勉強している本に、John W. Tukey（テューキー）のExploratory Data Analysis（探索的データ解析）があります。テューキーはアメリカの数学者、統計学者で、仮説検定ばかりが重視されていた時代に、記述統計学の重要性をうったえ、ロバスト統計学への流れを創った人物です。統計学のピカソと言われているくらい、統計学の様々な分野に業績を残しています。統計学以外の分野にもいくつも業績があり、例えば、高速フーリエ変換なども彼の業績の一つです。このような輝かしい業績の割には、日本ではあまり知られていません。探索的データ解析は700ページ近い大著で、1977年に出版されていますが、未だに翻訳されていないのが残念です。中を見ると、見慣れない手書きのグラフや数字の羅列がやたらと出てきます。箱ひげ図が紹介されたのもこの本です。おもしろいことに、数学的業績の多いテューキーの本とは思えないくらい、難解な数式は一つも出てきません。本の表やグラフで使われているほとんど全ての数値データは実際のデータであり、エネルギー、自動車といった産業界から化学、地理といった学問領域にまで亘っています。こうした広い領域で数値データを見てきたからこそ、探索的データ解析に辿り着いたのではないかと思えるほど、多様性に富んだデータが扱われています。
今日から何回かに分けて、探索的データ解析の本の中からソフトウェア関連の数値データの分析に役立ちそうなものを、このブログで紹介していきたいと思います。１回目の今日は、探索的データ解析の内容ではありませんが、探索的データ解析の手法と比較するために、ヒストグラム（度数分布図）を説明しておきます。以下のデータは、あるソフトウェアシステムの構成要素毎の詳細設計書枚数です。
285, 38, 321, 1060, 501, 1080, 136, 265, 106, 986, 45,
471, 422, 185, 1072, 269, 889, 2453, 82
このデータのヒストグラムを描くには、Excelのアドインにある分析ツールの中のヒストグラムを使います。ヒストグラムを描くときにいつも悩むのは、いくつの区間に分けるかということです。区間の数を決めるための方法として、スタージェスの公式など一般的な方法はいろいろあるようですが、どんなデータでもこの方法でよいといった万能の方法はありません。実際には、理論的な分布が分かっているような場合を除いては、対象とするデータとその特性などを考えながら、データに応じて試行錯誤を繰り返して決めることになると思います。ここでは、とりあえず、１００枚を一つの区間としてヒストグラムを描いてみました。
次回は、探索的データ解析の中で紹介されている幹葉図 (stem-and-leaf) を、このヒストグラムと対比する形でご紹介したいと思います。
フィード
Follow